Note: This paper comparing two different kinds of auction systems for IPOs was written for Yale Computer Science 455: Economics & Computation. The first and only auction-based IPO was for Google in 2004. Despite Google's established brand even in 2004, it priced at the low end of estimates and still increased 17% on the first day, which is not what one would expect with an auction designed to establish the best price at the IPO. Since then, companies have been more worried about completing a successful IPO than trying to pioneer new pricing techniques. Maybe Facebook will use an auction-based IPO to ensure that all users have access to stock at the IPO, not just the best customers of the lead underwriter.

Incentive-Compatible Initial Public Offerings

Eric Kennedy May 8th, 2002

Introduction

An Initial Public Offering, or IPO, is the financial event where a previously privately-held company sells common stock and is then listed on a major stock exchange. There are two principal reasons why a company enters the IPO market: to provide liquidity for the founders, venture capitalists, and employees with existing stock holdings; and to obtain new funds for the the company's use[6].

Traditionally, a company will hire an investment banking firm, such as Goldman Sachs or Morgan Stanley, to lead the promotion and underwriting of an IPO. After the U.S. Security and Exchange Commission (SEC) has approved the offer, the issuing company and its investment banker agree on a price and quantity for the firm's IPO shares (with an additional overallotment provision that gives the investment banker the option to sell as many as 15% more shares)[5]. After a price has been set, shares cannot be sold at a higher price even if the number of shares demanded at the offering price greatly exceeds the agreed-upon quantity[5]. Issuing IPO shares under this system is very expensive for the company, with a total cost of 7% of the gross proceeds going to underwriter commissions; legal, printing, and auditing expenses; and other out-of-pocket costs[5].

However, because the price of the IPO shares is fixed, the company cannot receive more proceeds even if the demand was greatly underestimated. Even in the average case, IPO shares appreciate more than 15% from the issue price to the first trade on the stock exchange[6]. This raises the question whether an auction for IPO shares could yield more profit for the company while also offering other advantages intrinsic to certain kinds of auctions. The traditional IPO mechanism violates the Consumer Sovereignty principal of incentive-compatible, deterministic auctions because an investor with the highest valuation who bids that valuation will not necessarily receive shares even if her valuation exceeds the offer price[6]. While some countries, such as England, require underwriters to distribute shares impartially, underwriters in the U.S. are allowed to allocate the majority of the shares to their most profitable customers[6].

This traditional system of IPO pricing may change, however, as one company has already created a new auction-based IPO pricing mechanism. In 1999, W.R. Hambrecht & Co introduced OpenIPO, an IPO pricing mechanism based on the incentive-compatible k-item Vickrey auction. That auction sells k items to the top k bidders, where each bidder pays a price equal to the bid value of bidder k+1[7]. It is also the only sealed-bid, single-round auction for k identical items where bidding one's valuation is incentive-compatible[1].

While the k-item Vickrey auction offers incentive compatibility, Fiat et al. note that there are situations where the auctioneer could obtain more revenue by selling fewer than k items[1]. Because IPOs are often postponed when the demand for a company's shares appears insufficient, they consider a subset of truthful auctions where the auctioneer can cancel the auction while still offering incentive-compatibility. They then propose the Sampling Cost Sharing (SCS) Auction as an example of a cancellable auction, and prove that it can produce an expected profit of between 1/4 and 1/2 of an optimal profit-maximizing auction for a restricted class of input data[1]

It is impossible to precisely compare the traditional IPO pricing mechanism against standard auction types, as that mechanism is based as much on an investment banker's intuition as on any consistent algorithm. Instead, I will compare the incentive-compatible (but not constant competitive) k-item Vickrey auction used by the OpenIPO mechanism, the incentive-compatible and constant competitive SCS auction, and the optimal (but not incentive-compatible) single-price auction.

To evaluate these three auctions, the Microsoft SQL Server database system was programmed to generate data, run auctions, and compare results. The methods used to generate data are explained in the next section, and the procedures themselves are included in the Appendix.

Data Generation Methods

To evaluate these mechanisms, bids with the following data were generated:

valuation in dollars, expressed to two decimal places
bid quantity, representing blocks of 100 shares

Bid Distribution Heuristics

The discount seen in IPO prices has been explained by K. Rock as a discount included to attract uninformed investors[6]. There are two classes of IPO investors: savvy institutional money-managers, and uninformed retail investors[6]. Uninformed investors need discounted prices as an incentive to participate because their lack of IPO investing experience and Wall Street knowledge make them susceptible to the winner's curse[6]. When informed investors have a high demand for an IPO, the underwriter can receive bids for many times the number of shares to be offered. This leads to rationing, which prevents uninformed investors from receiving some or all of the shares they bid for. However, when informed investors shun an IPO, uninformed investors are allocated all of the shares they bid for. After the IPO, informed investors continue to shun the company, leading to poor performance for the stock. Because uninformed investors receive a larger percentage of the shares they bid for when (in retrospect) it is undesirable to own the stock, receiving all of the shares one bids for is actually a curse, as it implies that the stock will underperform. According to this theory, uninformed investors will respond rationally by bidding a price that is their valuation minus some discount to compensate for their greater level of uncertainty in the future price of the stock[6].

Rock's theory suggests that there are two types of bid distributions for IPO shares: "hot" issues will have two superimposed bid distributions, one each for the informed and uninformed investors; "cold" issues will have only one bid distribution, as the informed investors will shun the issue. Note that in the case of "hot" issues, it is enough to assume that there are two bid distributions, without requiring that the bids for uninformed investors be distributed around a lower price than the bids of the informed investors. While it is also possible that there are three or more points around which groups of bids are distributed, as the number of these points becomes arbitrarily large, the resultant distribution of all bids can be approximated by a distribution of bids around a single point. For simplicity, only bids with distributions around one and two points will be considered.

Distributions Considered

The two bid distributions that will be considered are the normal distribution and a random distribution. Note that the following input values to the data generation procedures were chosen because they seemed reasonable and adequately representative of the kinds of distributions that might occur in an IPO.

The class of normal distributions, whose curve is given by the equation

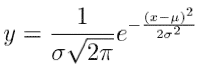
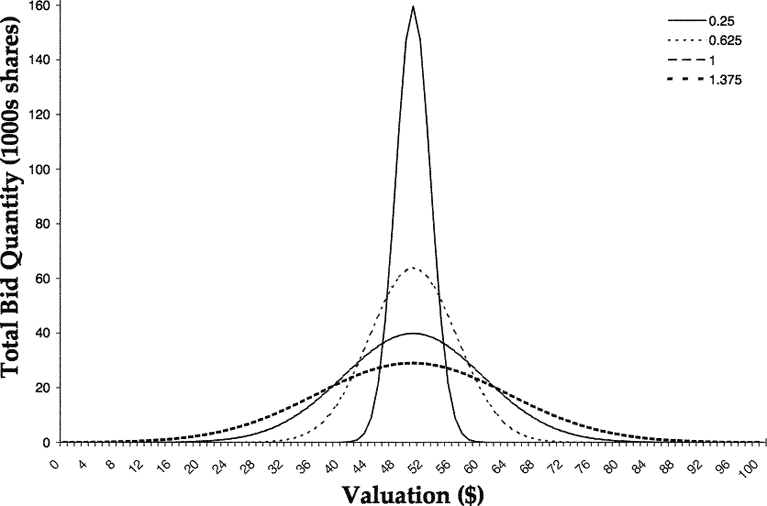
will be used to determine the number of bids y (each for 1,000 shares) at the valuation x[3]. Four different values (0.25, 0.625, 1.0, 1.375) for the standard deviation σ will be used to yield four output bid distributions for the single-point normal distribution. (Note that the mean μ is this single point.) Normally, a mean μ=0 would reflect a normal distribution centered around the origin. For these experiments, the mean has been re-centered to $50. Figure 1 shows overlaid graphs of the four single-point output bid distributions.

Figure 1: The four single-point output distributions for different values of σ.

In the two-point case, each point is the mean μ of a normal distribution curve. The values of both points, which correspond to two valuations, determine the offset of the two curves, and therefore affect the output bid distribution. The four offset values that will be used are: $5, $10, $20, and $30. All 16 combinations of these values will be used for each value of σ, yielding a total of 64 output bid distributions for the two-point normal distribution.

A random distribution of bid quantities and valuations will be generated by scaling the [0,1] output range of the Microsoft SQL Server RAND() function. Four values (10, 20, 32, and 64) will be used for the scaling factor for the the bid valuation for each random interval (bid quantities will have a fixed scaling value), and four values ($5, $10, $20, and $30) will be used for the offset distance between the start of the two random intervals. Because the bid quantities have a fixed scaling value, the order of the two intervals in the two-point case is irrelevant. Thus the total number of output bid distributions produced for the two-point case is 40, while four output bid distributions are produced for the one-point case. See Figure 2 for an illustration of a two-point random bid distribution.

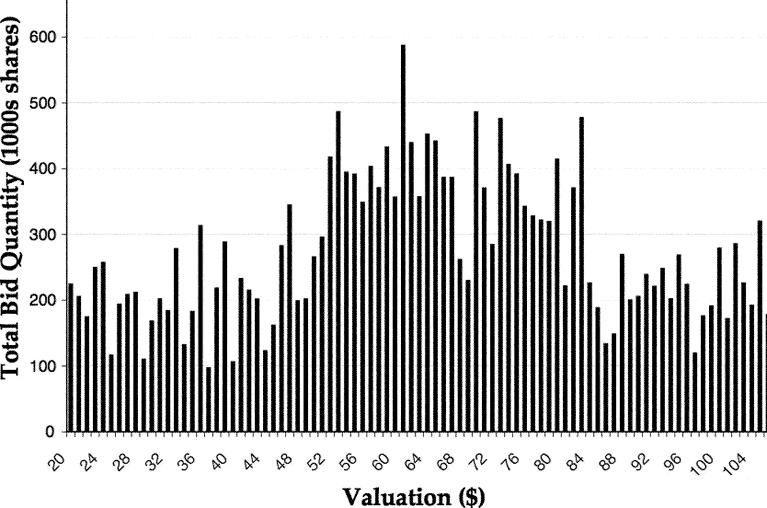
Figure 2: Two-point random bid distribution with a scaling factor of 64 applied to both random distributions and an offset distance of $30 between the start of the two random intervals.

Discussion of Results

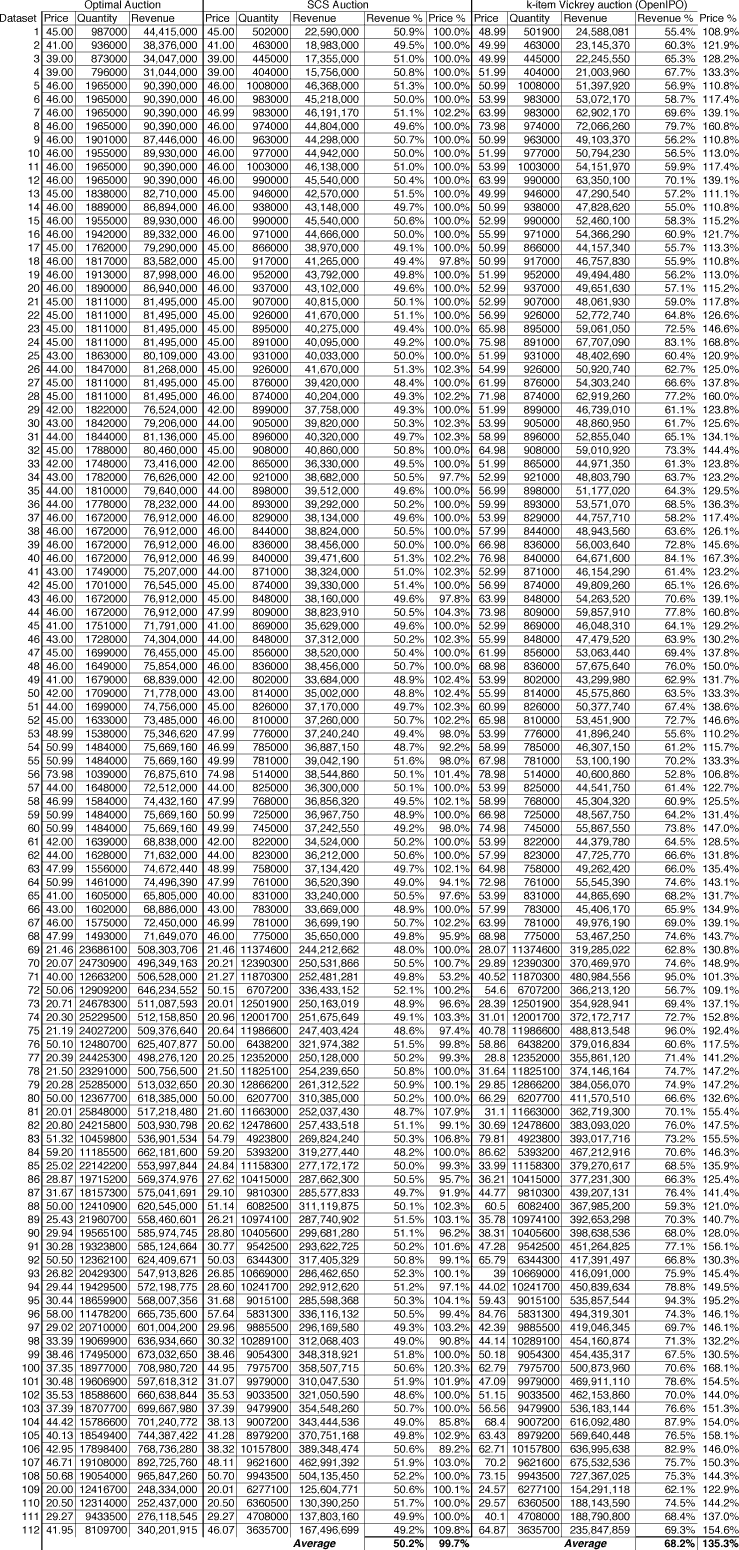
The three auction mechanisms were run on a total of 112 different bid distributions, with a grand total of 215,377 bids or 1,923 bids on average. To provide a comparison between the k-item Vickrey auction and the SCS auction, the value of k was chosen to be equal to the quantity sold by the SCS auction. Thus, the k-item auction's revenue can be compared to the SCS auctions revenue for the same number of shares sold. Because the quantity is fixed, the only way that the k-item auction could obtain a different revenue from the SCS auction is by charging a different price. As Figure 3 shows, the price charged by the k-item auction was in fact higher than the SCS and optimal auction price for all 112 bid distributions. Even though both the k-item and SCS auctions are incentive-compatible, the k-item Vickery auction will charge a higher price and obtain a higher revenue for the same number of shares sold.

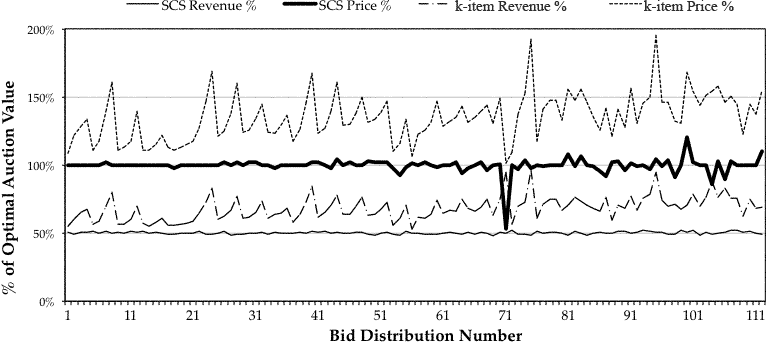
Figure 3: The revenue and price calculated by the SCS and k-item mechanisms as compared with the revenue and price of the optimal auction.

As the table of auction results in Appendix B shows, the average revenue obtained by the SCS auction was 50.2% of the optimal auction's revenue, while the price was 99.7% of the optimal auction's price. The average revenue of the k-item Vickrey auction was 68.2% of the optimal auction's revenue, while the price was 135.3% of the optimal auction's price. Thus, the price and revenue of the k-item Vickrey auction are 35% higher than the SCS auction for the same number of shares sold. These results suggest that the average-case revenue obtained by the SCS auction will be about one-half of the revenue of the optimal single-price auction, while the k-item Vickrey auction will obtain approximately two-thirds of the optimal auction revenue.

The SCS auction does not offer good revenue-maximizing properties in the average case, considering that the k-item Vickrey auction obtains approximately one-third more revenue for the same number of items sold. However, there is a reason why companies should, if given the choice, choose the SCS auction over a k-item Vickrey auction. One of the main criticisms of the k-item Vickrey-auction-based OpenIPO mechanism is that it removes the unmet demand that is preset in a traditional IPO. The same can be said for the optimal auction: by satisfying all of the bidders with the highest valuations, only the bidders with lower valuations will remain. Thus, few investors will be willing to buy the stock at a higher price than the IPO price after an optimal or k-item Vickrey auction. In contrast, the SCS auction would guarantee a significant amount of unmet demand by allocating shares to only half of the highest bidders. Thus, a company could expect that a significant number of the high bidders who did not receive shares in the IPO would buy shares on the exchange if the stock's price did not rise dramatically. This residual demand at the IPO price will provide a significant level of support under the stock, reducing the likelihood that it will fall below the IPO price onces it begins trading on an exchange.

Although the revenue that a company could collect with the SCS auction would be half that of the optimal auction, a company with a strong stock can easily conduct a secondary public offering within a year of the IPO. Thus, if the SCS auction contributes to the strength of the stock by insuring unmet demand, then this concern over IPO revenue may prove to be myopic.

While the SCS auction itself does not satisfy the principle of Consumer Sovereignty, neither does the traditional IPO mechanism. However, because IPO bidders can always purchase the stock on the exchange (albeit at a higher price) if they do not receive an allocation in the IPO, Consumer Sovereignty is satisfied when the IPO and exchange-trading are considered together.

Conclusion

The Sampling Cost Sharing auction proposed by Fiat et al is incentive-compatible, cancelable, and constant competitive with the optimal auction for any set of bid valuations. While the revenue that it raises is limited to one-half of the optimal auction's revenue, it obtains this revenue at approximately the same price as the optimal auction. Consequently, a significant amount of unmet demand remains after the SCS auction has completed, ensuring that that are still investors willing to buy the stock at or above the IPO price after the IPO. Further, it provides a worst-case revenue guarantee of one-quarter of the optimal revenue, while the k-item Vickrey auction implemented by W.R. Hambrecht & Co.'s OpenIPO mechanism cannot provide any constant revenue guarantee. With these advantages, the SCS auction is well suited to the problem of pricing and allocating shares in IPOs.

Appendix A: SQL Server Stored Procedures

GenNormalDist

CREATE PROCEDURE GenNormalDist @IPOID tinyint, @valSD float, @valMean float AS
/* For the 'two-point' case, this function is called twice with the same 
 * @IPOID value but different @valSD and @valMean values 
 *  NOTE: valMean should be called with 1/10 the intended value */

DECLARE @Valuation float, @x float, @numBidders float, @expVal float
SET @x = 0
WHILE @x < 10
BEGIN
     SET @numBidders = 0; SET @expVal = 0; 

     /* determine the exponent for e (Note Valuation is shifted right by 5)*/
     SELECT @expVal = - POWER(@x - 5 - @valMean, 2)/(2*POWER(@valSD, 2))

     /* calculate the number of 1000 share bidders at this point */
     SELECT @numBidders = (100/(@valSD * 2.506)) * POWER(2.71828, @expVal)

     SET @Valuation = 1000 * @x
     WHILE @numBidders > 0.5
     BEGIN
          INSERT INTO tblBidders (IPOID, Valuation, QuantityDemanded)
               VALUES (@IPOID, CAST(@Valuation AS smallint), 10 )
          SET @numBidders = @numBidders - 1
     END

     SET @x = @x + 0.1
END

GenRandomDist

CREATE PROCEDURE GenRandomDist @IPOID tinyint, @valScale smallint, @valStart smallint AS
/* For the 'two-point' case, this function is called twice with @valStart values
 * that differ by the random interval offset value */

DECLARE @i int, @Valuation float, @QuantityDemanded float

SET @i = 0
WHILE @i < 1000
BEGIN

     /* valuation will range from from @valStart to @valStart + @valScale */
     SELECT @Valuation = @valScale * RAND()  + @valStart

     /* quantity will range from 1 (100 shares) to 255 (25,500 shares) */
     SELECT @QuantityDemanded = 255 * RAND()
	
     INSERT INTO tblBidders (IPOID, Valuation, QuantityDemanded)
     VALUES (@IPOID, CAST(@Valuation AS smallint), CAST(@QuantityDemanded as tinyint) )

     SET @i = @i + 1
END

SCSAuction


CREATE PROCEDURE SCSAuction @IPOID tinyint AS

DECLARE @totalRevenue int, @lastValuation smallint, @partitionVal BIT,  @thisRand float
DECLARE @userValuation smallint, @bidderID int, @lastRand float, @quantityDemanded tinyint
DECLARE @totalSold int

DECLARE valList CURSOR LOCAL STATIC FOR
SELECT BidderID FROM tblBidders WHERE IPOID=@IPOID
OPEN valList

SET @lastRand = 0; SET @thisRand = 0

FETCH FROM valList INTO @bidderID
WHILE @@FETCH_STATUS = 0
BEGIN
     SET @thisRand = RAND()
     IF ( @thisRand > @lastRand )
          UPDATE tblBidders SET SCSPartition = 1 WHERE BidderID=@bidderID
     ELSE
          UPDATE tblBidders SET SCSPartition = 0 WHERE BidderID=@bidderID
     SET @lastRand = @thisRand

     FETCH NEXT FROM valList INTO @bidderid
END

DEALLOCATE valList

SET @totalRevenue = 0; SET @lastValuation = 0; SET @partitionVal = 0; SET @totalSold = 0

EXEC SCSOptimalAuction @IPOID, @partitionVal, @lastValuation OUTPUT, @totalRevenue OUTPUT

IF @totalRevenue = 0  /* no winners, so run SCSOptimalAuction on the other partition */
BEGIN
     SET @partitionVal = 1
     EXEC SCSOptimalAuction @IPOID, @partitionVal, @lastValuation OUTPUT, @totalRevenue OUTPUT
END

UPDATE tblBidders SET SCSAllocation = 0 WHERE IPOID=@IPOID  /* clear existing allocation */

UPDATE tblBidders SET SCSAllocation=QuantityDemanded 
     WHERE SCSPartition = @partitionVal AND IPOID=@IPOID AND Valuation >= @lastValuation

SELECT @totalSold = SUM(SCSAllocation) FROM tblBidders
     WHERE SCSPartition = @partitionVal AND IPOID=@IPOID

INSERT INTO tblAuctionResults (IPOID, AuctionType, SettlePrice, QuantitySold, TotalRevenue)
VALUES (@IPOID, 3, @lastValuation, @totalSold, @totalRevenue)

SCSOptimalAuction

CREATE PROCEDURE SCSOptimalAuction
@IPOID tinyint, @partitionVal BIT, @lastValuation smallint OUTPUT, @totalRevenue int OUTPUT
AS

DECLARE @valuation smallint, @quantity tinyint, @auctionType tinyint, @totalQuantity int

/* create a temporary table for the quantity available at each valuation */
CREATE TABLE #tmpTable (Price smallint, TotalRevenue int, TotalSold int)
INSERT INTO #tmpTable
     SELECT DISTINCT(Valuation) AS Price, 0 AS TotalRevenue, 0 AS TotalSold 
     FROM tblBidders WHERE IPOID = @IPOID AND SCSPartition = @partitionVal

DECLARE valList CURSOR LOCAL STATIC FOR
SELECT Valuation, QuantityDemanded FROM tblBidders
WHERE IPOID=@IPOID AND SCSPartition = @partitionVal
ORDER BY Valuation DESC
OPEN valList

SET @totalRevenue= 0; SET @lastValuation = 0; SET @totalQuantity = 0

FETCH FROM valList INTO @valuation, @quantity
WHILE @@FETCH_STATUS = 0
BEGIN
     /* this user is willing to buy at any price less than or equal to her valuation */
     UPDATE #tmpTable SET TotalSold = TotalSold + @quantity
          WHERE Price <= @valuation

     FETCH NEXT FROM valList INTO @valuation, @quantity
END

UPDATE #tmpTable SET TotalRevenue = TotalSold * CAST(Price as int)

/* Now select the max revenue */
SELECT TOP 1 @lastValuation = Price, @totalRevenue = TotalRevenue, @totalQuantity = TotalSold
FROM #tmpTable ORDER BY TotalRevenue DESC

DEALLOCATE valList
DROP TABLE #tmpTable

OptimalAuction

CREATE PROCEDURE OptimalAuction @IPOID tinyint AS

DECLARE @valuation smallint, @quantity tinyint
DECLARE @price smallint,  @totalRevenue int, @totalQuantity int

/* create a temporary table for the quantity available at each valuation */
CREATE TABLE #tmpTable (Price smallint, TotalRevenue int, TotalSold int)
INSERT INTO #tmpTable 
     SELECT DISTINCT(Valuation) AS Price, 0 AS TotalRevenue, 0 AS TotalSold
     FROM tblBidders WHERE IPOID = @IPOID

DECLARE valList CURSOR LOCAL STATIC FOR
SELECT Valuation, QuantityDemanded FROM tblBidders WHERE IPOID=@IPOID
ORDER BY Valuation DESC
OPEN valList

SET @totalRevenue = 0; SET @price = 0; SET @totalQuantity = 0

FETCH FROM valList INTO @valuation, @quantity
WHILE @@FETCH_STATUS = 0
BEGIN
     /* user is willing to buy at any price less than or equal to her valuation */
     UPDATE #tmpTable SET TotalSold = TotalSold + @quantity
             WHERE Price <= @valuation

     FETCH NEXT FROM valList INTO @valuation, @quantity
END

UPDATE #tmpTable SET TotalRevenue = TotalSold * CAST(Price as int)

/* Now select the max revenue */
SELECT TOP 1 @price = Price, @totalRevenue = TotalRevenue, @totalQuantity=TotalSold 
     FROM #tmpTable ORDER BY TotalRevenue DESC

UPDATE tblBidders SET OptimalAllocation = QuantityDemanded
     WHERE Valuation >= @price AND IPOID=@IPOID

INSERT INTO tblAuctionResults (IPOID, AuctionType, SettlePrice, QuantitySold, TotalRevenue)
VALUES (@IPOID, 2, @price, @totalQuantity, @totalRevenue)

DEALLOCATE valList
DROP TABLE #tmpTable

OpenIPO: a single-price k-item Dutch auction

CREATE PROCEDURE OpenIPO @IPOID tinyint, @k INT AS

DECLARE @valuation smallint, @quantity int, @fillRatio float
DECLARE @price smallint,  @totalRevenue int, @totalQuantity int

DECLARE valList CURSOR LOCAL STATIC FOR
SELECT DISTINCT(Valuation) AS Valuation, SUM(CAST(QuantityDemanded as int)) AS Quantity
FROM tblBidders WHERE IPOID = @IPOID GROUP BY Valuation, QuantityDemanded
ORDER BY Valuation DESC
OPEN valList

SET @totalRevenue = 0; SET @price = 0; SET @totalQuantity = 0

FETCH FROM valList INTO @valuation, @quantity
WHILE @@FETCH_STATUS = 0
BEGIN
     SET @price = @valuation /* in case there are no more rows */
     IF (@totalQuantity + @quantity < @k) /* all bids at this valuation get allocated */
     BEGIN
          UPDATE tblBidders SET VickreyAllocation=QuantityDemanded WHERE Valuation = @valuation
          SET @totalQuantity = @totalQuantity + @quantity
     END
     ELSE /* some bids at this valuation will get allocated */
     BEGIN
          SET @fillRatio = CAST((@k - @totalQuantity) as float)/(CAST(@quantity as float))
          UPDATE tblBidders SET VickreyAllocation = CAST( (QuantityDemanded * @fillRatio) as tinyint)
               WHERE Valuation = @valuation
          SET @totalQuantity = @totalQuantity + CAST((@quantity * @fillRatio) as int)
          /* now get the k+1st price */
          FETCH NEXT FROM valList INTO @valuation, @quantity
          IF @@FETCH_STATUS = 0
          BEGIN
               SET @price = @valuation /* the k+1st price */
               BREAK
          END  /* if @@FETCH_STATUS != 0, we can use the existing @Price value */
     END     
     FETCH NEXT FROM valList INTO @valuation, @quantity
END

SET @totalRevenue = @totalQuantity * @price

INSERT INTO tblAuctionResults (IPOID, AuctionType, SettlePrice, QuantitySold, TotalRevenue)
VALUES (@IPOID, 1, @price, @totalQuantity, @totalRevenue)

DEALLOCATE valList

Appendix B: Table of Auction Results

Bibliography

A. Fiat, A. Goldberg, J. Hartline, and A. Karlin. Competitive Generalized Auctions. To appear STOC 2002. Available at http://www.math.tau.ac.il/ fiat/stocauc.ps
W. R. Hambrecht & Co. http://www.wrhambrecht.com
Wolfram Research. http://mathworld.wolfram.com/GaussianDistribution.html
Ravenswood Winery, Inc. Stockholders Approve Merger With Constellation. PR Newswire. Financial News. Lexis-Nexis. Yale University Lib., New Haven, CT. 26 June 2001.
J. Ritter. The Costs of Going Public. In Journal of Financial Economics, Vol. 19, No. 2 (December 1987), pp. 269-81.
K. Rock. Why New Issues Are Underpriced. In Journal of Financial Economics, Vol 15, (1986) pp. 187-212.
W. Vickrey. Counterspeculation, Auctions, and Competitive Sealed Tenders. In Journal of Finance, 1961.